Introduction to Quantum Mechanics

Quantum Mechanics (QM)

In quantum physics, some things appear to be probabilistic (i.e. random). For example, all elementary particles (like photons and electrons) have an intrinsic spin (this has been experimentally confirmed). If you measure that spin from a specific angle, it can be either “up” or “down” (since there are two possible values, we call this a quantum bit, or a qubit).

In classical mechanics, if you wanted to predict the spin, you might ask questions like “where was the particle a few seconds ago?” and “have any forces acted on it to give it angular momentum?” But in quantum mechanics, these questions make no sense. As far as we can tell, the spin is random.¹² We call this quantum indeterminacy.

As an engineer, there is something fundamentally confusing about that statement. In our day-to-day lives, everything we experience is governed by classical mechanics (think: Newton’s laws of motion). We’re so comfortable with these mechanisms that the idea of “random” behavior is incredibly hard to grasp.

Scientists are still asking a lot of questions about QM, but there are a lot of things we already know.

The Double Slit Experiment

I vaguely remember the double-slit experiment from high school, but when revisiting this, I realized I missed out on some major implications. I think it’s important to understand what’s really going on.

The Double Slit experiment primarily shows the wave-particle duality of photons (light), an example of a wave function, and what wave function collapse looks like.

Single-Slit

First is the single-slit experiment: When you shine a light (which is really a stream of individual photons) through a single slit to a back wall, you get a diffraction pattern. This is characterized by one very bright “band” of light on the back wall, and several gradually dimmer “bands” in a pattern moving away from the central band.

NOTE: Even in this simple experiment, we can see the wave-particle duality of light: while only individual photons are detected on the back wall, they scatter like a wave.

Double-Slit

Next is the double-slit experiment: If you introduce a 2nd slit, the photons coming out the two slits appear to interfere with each other, causing a pattern of light and dark bands on the back wall. We call this an interference pattern. It’s kinda like splashing two waves in a still pool, and watching the waves interfere with one another.

Double-Slit, One Photon at a Time

What would happen if we “downgraded” our light to an extremely weak laser that only emits a single photon at a time? Since the photons won’t be interfering with each other anymore, maybe they’ll just “pick” one of the slits to go through, and form a diffraction pattern behind it. That would look something like this:

But, this is not what we observe. Even though only one photon is traveling through the double-slit system at a time, the back wall still shows an interference pattern! It’s as if the individual photon is interfering with itself!

Adding Photon Detectors

Finally, we introduce “photon detectors” at each of the two slits to tell us when a photon is passing through that slit. Suddenly, the interference pattern totally disappears! We call this a wave function collapse, because now the photons have been measured, and are no longer acting as waves. Instead, we get two diffraction patterns!

The Measurement Problem

Scientists don’t know why the wave function collapse occurs at measurement. We call this the measurement problem, and it asks questions like:

• Why does the wave function collapse at measurement?
• What happens during the wave function collapse? It it real, or just apparent?
• What kind of measurement counts?
• Does measurement require consciousness?

All valid interpretations of quantum mechanics must answer the measurement problem.

Wave Function

What is a photon? What does it look like?

If you’re imagining a tiny sphere, you’ve only got it partially right. Before a photon is measured, we don’t really know where, or what, it really is. We call this state a superposition, meaning there are multiple possible options (called eigenstates), all real at the same time. In this pre-measured state, all we know is that a photon tends to appear in specific locations. In other words, we can make some generic statements about a pre-measured photon, but it may not “exist” as a particle yet.

In this pre-measured state, we can describe quantum particles as a wave function. A wave function is just a way of encoding a particle’s probabilistic nature into a mathematical function. This is useful, because we can do math on wave functions.

When a wave function is measured (e.g. a photon’s position), it experiences wave function collapse, where the wave function “collapses” from a wave of probability into a single eigenstate.

Schrödinger Equation: Predicting Probability

Now that we’re encoding quantum systems into our mathematical model, the wave function, we can do some useful math on them. Even if quantum particles (modeled using a wave function) appear to behave probabilistically, we can use the Schrödinger equation to model predict how those probabilities change over time.

For example, let’s say you trap an electron in a box. When you open the box, where will it be? Because electrons behave according to a wave function, it’s impossible to predict with certainty where it will be, but we can use the Schrödinger equation to calculate the likelihood the electron will be in any specific spot. The Schrödinger equation can also predict a wave function’s probabilities at specific points in time.

A key part of the Schrödinger equation is unitarity: while a wave function is alive (i.e. before its collapse), its list of possibilities remains the same. A wave function cannot gain a newly possible outcome, or lose an existing one.

Using the Schrödinger equation, we can show that the probabilistic behavior of a wave function changes deterministically.

Hidden Variables?

As far as we can tell, quantum systems are behaving randomly. But what if we’re just not smart enough to predict what the photon will do? What if there’s some hidden information or variable we’re just not considering? Like, maybe each photon stores information about where it’s been, and where it will go next. Even Einstein doubted that quantum systems are truly random, stating that “God does not play dice.”

In 1964, John Stewart Bell formulated Bell’s Theorem, which basically states that if quantum systems are using hidden variables, there would be limits on how correlated measurements of entangled particles could be. These limits are called Bell inequalities. Thanks to later experiments done by physicists like Alain Aspect, John Clauser, and Anton Zeilinger (who all won the 2022 Nobel Prize in Physics), we have experimentally showed that quantum systems violate Bell inequalities, thus ruling out any local hidden variable theory.

Bell’s Theorem, and the resultant experiments, helped set limits for acceptable interpretations of quantum mechanics.

Quantum Entanglement

When scientists do experiments on wave functions and qubits, entangled particles are frequently involved. If one wave function is indescribable apart from another wave function, those two wave functions are said to be entangled. In other words, observing one wave function will tell you something about the other, instantly, no matter how far apart they are.

It’s incredibly easy to entangle a wave function with something else: literally any interaction will work. As a simple example, imagine you obtain a qubit in superposition of spin up and spin down. When you observe the qubit to measure its spin, you both become “entangled” to an outside observer, who sees both you and the qubit as in one superposition (until you tell them what you saw).

There are multiple ways of creating a pair of entangled particles for experimentation. I’ll just dive into a real, ~40-year-old quantum entanglement method that scientists still use: the Hong Ou Mandel Effect.

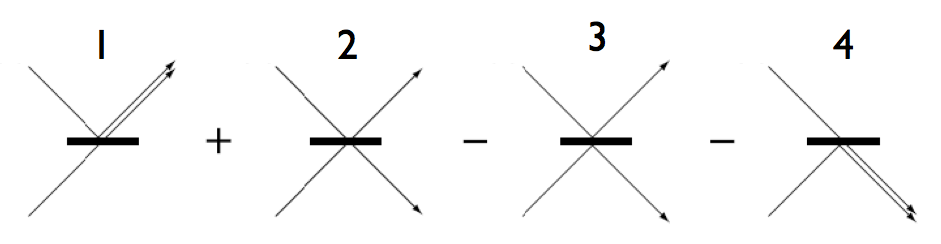
1. When a photon hits a special material called a beam splitter, it has a 50% chance of being reflected, and a 50% chance of passing through. This behavior is probabilistic; you cannot predict whether a specific photon will reflect, or pass through.
2. Imagine you shoot two identical photons at a beam splitter, from opposite directions.
3. If two photons arrive at a beam splitter at the same moment, there are 4 possible outcomes:³
   1. The photon coming in from above is reflected, and the photon coming in from below passes through.
   2. Both photons pass through.
   3. Both photons are reflected.
   4. The photon coming in from above passes through and the photon coming in from below is reflected.
4. Since the two photons are identical, outcomes 2 and 3 are indistinguishable, since you could never tell the photons apart.
5. Scientists have experimentally determined an equation to determine the likelihood that a quantum system will “choose” certain outcomes: you square the probability amplitude of the outcome. Since options 2/3 are equivalent in amplitude, but opposite in sign, they cancel out.
6. The only outcomes left are 1 and 4, which are also equivalent in amplitude. Thus, there’s a 100% chance the photons will exit together (aww).
7. If we measure a photon on top side, we immediately know the other photon is also on top side (outcome 2). If we measure a photon on the bottom side, we immediately know the other photon is also on the bottom side (outcome 4).
8. Congratulations! You’ve just entangled two photons.

Conclusion

Hopefully, you’ve learned some fundamental concepts of quantum mechanics. These terms and ideas are building blocks that lead to understanding some of the modern interpretations of quantum mechanics, and thus interpretations of how our world really works.